simpsons paradox in Python
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
import pandas as pd
# Define the data
data = {
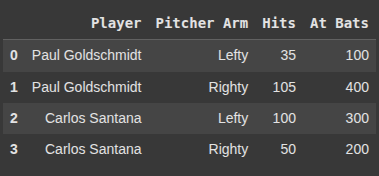
"Player": ["Paul Goldschmidt", "Paul Goldschmidt", "Carlos Santana", "Carlos Santana"],
"Pitcher Arm": ["Lefty", "Righty", "Lefty", "Righty"],
"Hits": [35, 105, 100, 50],
"At Bats": [100, 400, 300, 200],
}
# Create a DataFrame
df = pd.DataFrame(data)
df.head(5)
# Calculate batting averages
df['Batting Avg'] = df['Hits'] / df['At Bats']
# Aggregate total stats for each player
df_totals = df.groupby("Player").sum(numeric_only=True).reset_index()
df_totals['Batting Avg'] = df_totals['Hits'] / df_totals['At Bats']
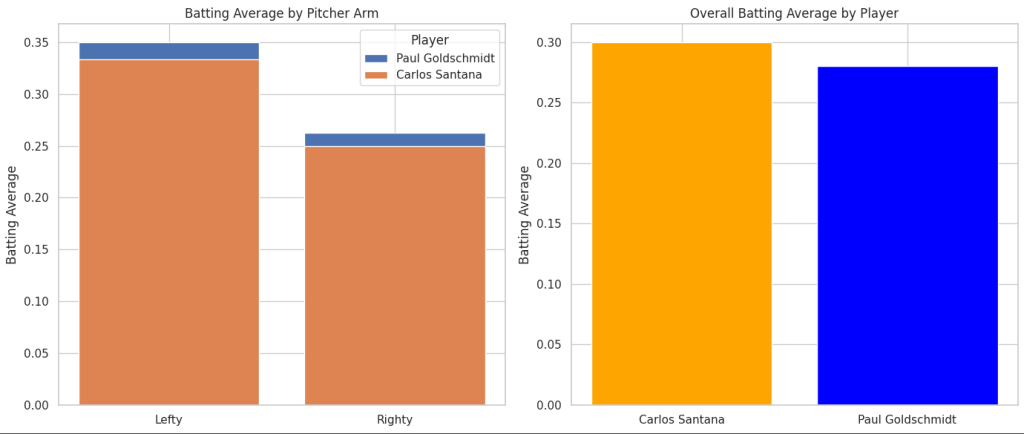
# Plot Batting Average by Pitcher Arm
fig, axes = plt.subplots(1, 2, figsize=(14, 6))
# Plot individual batting averages
for player in df['Player'].unique():
subset = df[df['Player'] == player]
axes[0].bar(subset['Pitcher Arm'], subset['Batting Avg'], label=player)
axes[0].set_title("Batting Average by Pitcher Arm")
axes[0].set_ylabel("Batting Average")
axes[0].legend(title="Player")
# Plot aggregated batting averages
axes[1].bar(df_totals['Player'], df_totals['Batting Avg'], color=['orange', 'blue'])
axes[1].set_title("Overall Batting Average by Player")
axes[1].set_ylabel("Batting Average")
plt.tight_layout()
plt.show()
2nd example Running
np.random.seed(42)
# Parameters for dataset
n_young = 500 # Number of young runners
n_old = 500 # Number of old runners
# Generate data for younger runners
young_miles = np.random.uniform(20, 65, n_young) # Miles ran per week
young_fastest_mile = 500 - 3 * young_miles + np.random.normal(0, 15, n_young) # Fastest mile time (better as mileage increases)
# Generate data for older runners
old_miles = np.random.uniform(20, 70, n_old) # Miles ran per week
old_fastest_mile = 800 - 1 * old_miles + np.random.normal(0, 15, n_old) # Fastest mile time (worse performance overall)
# Shift old runners to have higher mileage and worse times to create the paradox
old_miles += 5
old_fastest_mile += 20
# Combine data into a single DataFrame
data = pd.DataFrame({
"Miles Ran Per Week": np.concatenate([young_miles, old_miles]),
"Fastest Mile Time (seconds)": np.concatenate([young_fastest_mile, old_fastest_mile]),
"Age Group": ["Young"] * n_young + ["Old"] * n_old
})
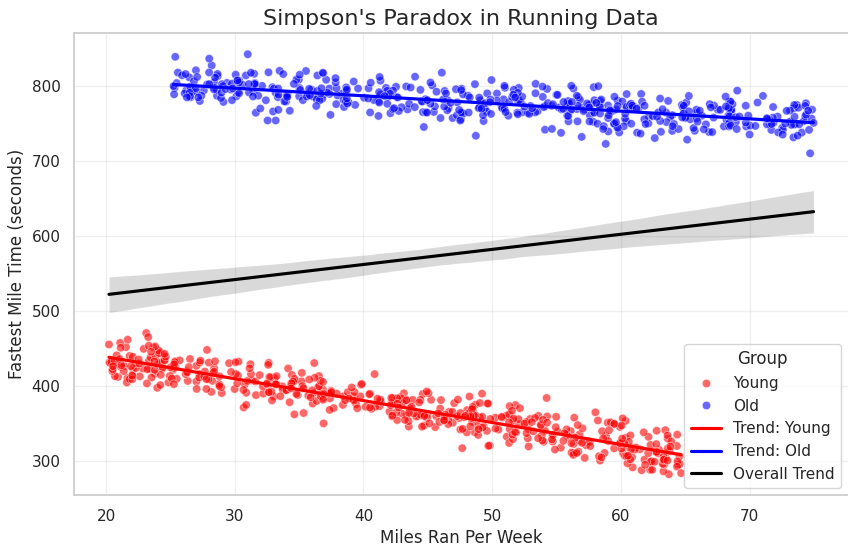
1st plot just the mile time/miles per week
# Plotting
plt.figure(figsize=(10, 6))
sns.scatterplot(
x="Miles Ran Per Week",
y="Fastest Mile Time (seconds)",
hue="Age Group",
data=data,
palette={"Young": "red", "Old": "blue"},
alpha=0.6
)
# Add trend lines for each group
sns.regplot(
x="Miles Ran Per Week",
y="Fastest Mile Time (seconds)",
data=data[data["Age Group"] == "Young"],
scatter=False,
color="red",
label="Trend: Young"
)
sns.regplot(
x="Miles Ran Per Week",
y="Fastest Mile Time (seconds)",
data=data[data["Age Group"] == "Old"],
scatter=False,
color="blue",
label="Trend: Old"
)
# Add overall trend line
sns.regplot(
x="Miles Ran Per Week",
y="Fastest Mile Time (seconds)",
data=data,
scatter=False,
color="black",
label="Overall Trend"
)
# Customize the plot
plt.title("Simpson's Paradox in Running Data", fontsize=16)
plt.xlabel("Miles Ran Per Week", fontsize=12)
plt.ylabel("Fastest Mile Time (seconds)", fontsize=12)
plt.legend(title="Group")
plt.grid(True, alpha=0.3)
plt.show()
