scipy chi square test of independence
#The Chi-Squared test determines whether there’s a significant association between categorical variables.
#It compares the observed frequencies (counts) to the expected frequencies, calculated under the null hypothesis that the variables are independent or that the observed distribution fits a given distribution.
#Chi-Squared Test for Independence
#This test checks if there’s an association between two categorical variables by comparing observed frequencies in a contingency table.
#Imagine we have a survey with data on the preferred coffee types by gender.
#We want to determine if there’s a relationship between gender and coffee preference.
#Step 1 – Create the Contingency Table
#Espresso Latte Black
#Male 30 20 50
#Female 35 25 30
#observed = np.array([[30, 20, 50], [35, 25, 30]])
#Step 2 – Run the Chi-Squared Test for Independence
#output
#Chi-Squared: 5.0943
#p-value: 0.0782
#Degrees of Freedom: 2
#Expected Frequencies:
#[[32.64 22.92 44.44]
# [32.36 22.08 45.56]]
#Since the p-value (0.0782) is greater than 0.05, we fail to reject the null hypothesis,
#suggesting there’s no significant association between gender and coffee preference
import numpy as np
import scipy.stats as stats
alpha = 0.05
Example 1 Manual Calculation #morning drink choice
observed = np.array([
[40, 30, 10], # Male
[80, 20, 20] # Female
])
row_totals = observed.sum(axis=1)
col_totals = observed.sum(axis=0)
grand_total = observed.sum()
print(grand_total)
# Step 1: Calculate expected values
expected = np.outer(row_totals, col_totals) / grand_total
print(expected)
# Step 2: Calculate the Chi-Squared statistic
chi_squared = ((observed - expected) ** 2 / expected).sum()
print(chi_squared)
# Step 3: Calculate the p-value
# Degrees of freedom = (rows - 1) * (columns - 1)
degrees_of_freedom = (observed.shape[0] - 1) * (observed.shape[1] - 1)
print(degrees_of_freedom)
p_value = 1 - stats.chi2.cdf(chi_squared, degrees_of_freedom)
print(p_value)
if p_value > alpha:
print("The two variables are independent (there is no association between them). fail to reject H0.")
else:
print("The two variables are dependent (there is an association between them). reject H0.")
Example 2 Shortcut
chi2, p, dof, expected = stats.chi2_contingency(observed)
print("Chi-Squared:", chi2)
print("p-value:", p)
print("Degrees of Freedom:", dof)
print("Expected Frequencies:\n", expected)
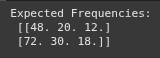
#p-value: If this value is less than our significance level (e.g., 0.05), we reject the null hypothesis
#and conclude an association exists
#expected: These are the expected frequencies under the null hypothesis
Example X 3 different Groups
#Suppose we want to investigate whether race distance preferance is associated with age group.
#We surveyed 200 people and categorized them by their age group and voting preference
# 5k marathon ultra marathon
#Under 30 50 30 20
#30-50 40 40 20
#Over 50 30 30 40
observed = np.array([[55, 30, 25],
[35, 30, 25],
[30, 40, 30]])
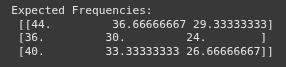
chi2, p_value, dof, expected = stats.chi2_contingency(observed)
print("Chi-Squared Statistic:", chi2)
print("p-value:", p)
print("Degrees of Freedom:", dof)
print("Expected Frequencies:\n", expected)
if p_value > alpha:
print("The two variables are independent (there is no association between them). fail to reject H0.")
else:
print("The two variables are dependent (there is an association between them). reject H0.")
