time series seasonality python
import matplotlib.pyplot as plt
import pandas as pd
from datetime import datetime
from statsmodels.tsa.stattools import adfuller
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
df = pd.read_csv('/content/86628_2010_1_1_2024.csv')
df.columns = df.columns.str.strip() # Remove leading/trailing spaces from column names
df.columns
df["Date"] = pd.to_datetime(df[["YEAR", "MONTH", "DAY"]], errors="coerce")
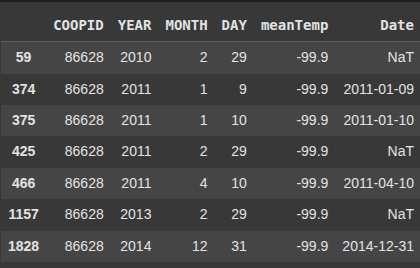
invalid_dates = df[(df["Date"].isna()) | (df['meanTemp'] < -10)]
invalid_dates
df = df.dropna(subset=["Date"])
df = df[df['meanTemp'] >= -10]
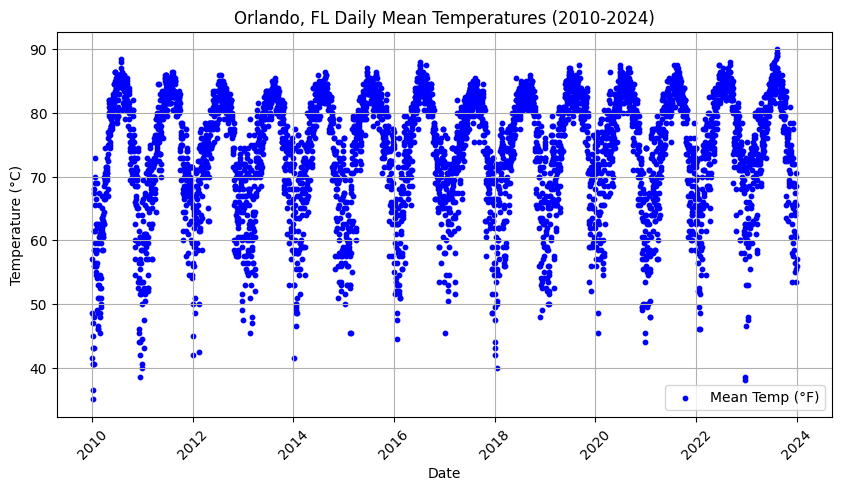
plt.figure(figsize=(10, 5))
plt.scatter(df["Date"], df["meanTemp"], color='b', label='Mean Temp (°F)', s=10) # s controls the size of the dots
# Formatting plot
plt.xlabel("Date")
plt.ylabel("Temperature (°C)")
plt.title("Orlando, FL Daily Mean Temperatures (2010-2024)")
plt.xticks(rotation=45)
plt.legend()
plt.grid()
plt.show()
Lets look at a specific year now
df[“Date”] = pd.to_datetime(df[“Date”])
df_filtered = df[(df["Date"] >= "2022-01-01") & (df["Date"] <= "2024-12-31")].copy()
adf_test = adfuller(df_filtered["meanTemp"].dropna()) # Drop NaNs if necessary
print("p-value:", adf_test[1])
# Interpretation
if adf_test[1] < 0.05:
print("The time series is stationary (reject H0).")
else:
print("The time series is not stationary (fail to reject H0).")
Summary Statistics by a Period (week, month, quarter etc)
def get_season(month):
if month in [12, 1, 2]:
return "Winter"
elif month in [3, 4, 5]:
return "Spring"
elif month in [6, 7, 8]:
return "Summer"
else:
return "Fall"
# Apply the function to create a new "Season" column
df_filtered["Season"] = df_filtered["Date"].dt.month.apply(get_season)
# Compute summary statistics by season
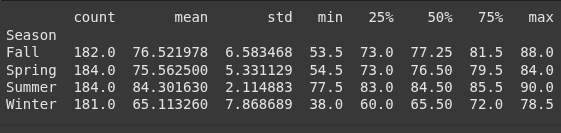
seasonal_stats = df_filtered.groupby("Season")["meanTemp"].describe()
# Display results
print(seasonal_stats)
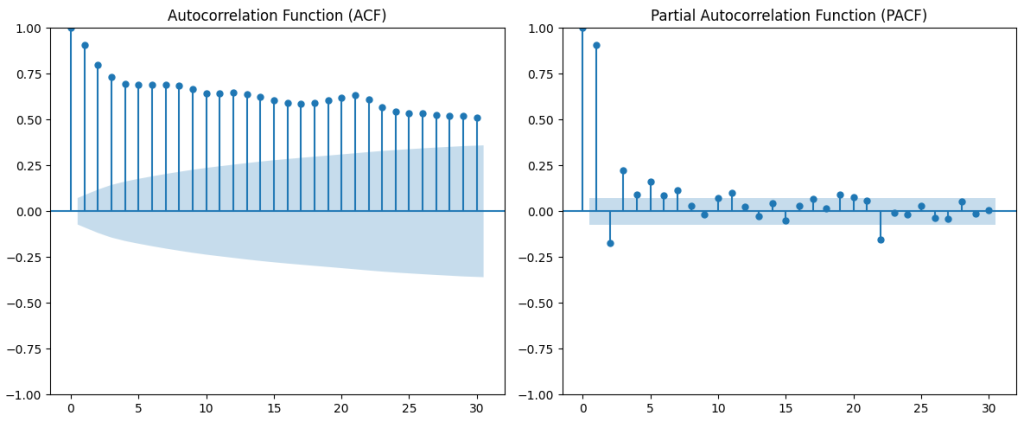
#acf and pacf report
# Set up figure for ACF and PACF plots
fig, axes = plt.subplots(1, 2, figsize=(12, 5))
# Plot ACF (Autocorrelation Function)
plot_acf(df_filtered["meanTemp"].dropna(), ax=axes[0], lags=30) # Adjust lags if needed
axes[0].set_title("Autocorrelation Function (ACF)")
# Plot PACF (Partial Autocorrelation Function)
plot_pacf(df_filtered["meanTemp"].dropna(), ax=axes[1], lags=30, method='ywm')
axes[1].set_title("Partial Autocorrelation Function (PACF)")
plt.tight_layout()
plt.show()
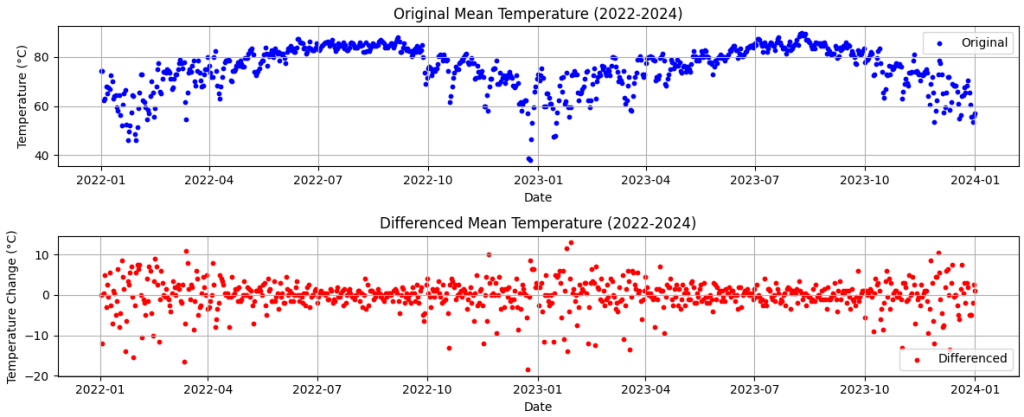
df_filtered["meanTemp_diff"] = df_filtered["meanTemp"].diff()
# Plot original and differenced series
plt.figure(figsize=(12, 5))
# Plot original time series
plt.subplot(2, 1, 1)
plt.scatter(df_filtered["Date"], df_filtered["meanTemp"], color='b', s=10, label="Original")
plt.xlabel("Date")
plt.ylabel("Temperature (°C)")
plt.title("Original Mean Temperature (2022-2024)")
plt.legend()
plt.grid()
# Plot differenced time series
plt.subplot(2, 1, 2)
plt.scatter(df_filtered["Date"], df_filtered["meanTemp_diff"], color='r', s=10, label="Differenced")
plt.xlabel("Date")
plt.ylabel("Temperature Change (°C)")
plt.title("Differenced Mean Temperature (2022-2024)")
plt.legend()
plt.grid()
plt.tight_layout()
plt.show()
