Ridge Regressor
#Ridge Regression which is considered
#L2 Regularization
#helps with overfitting in linear regression models
#keeping the coefficients small
# lead to a model that is less prone to overfitting
#balance between fitting the data and keeping the coefficients small
#more robust and stable models, particularly when dealing with datasets that have highly correlated predictor variables
from sklearn.datasets import make_regression X, y = make_regression(n_samples=100, n_features=4, noise=0.1, random_state=42, effective_rank=2) from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=19) from sklearn.preprocessing import StandardScaler scaler = StandardScaler() X_train = scaler.fit_transform(X_train) X_test = scaler.transform(X_test) from sklearn.linear_model import Ridge ridge = Ridge() ridge.fit(X_train, y_train) 
from sklearn.metrics import mean_absolute_error, mean_squared_error, r2_score y_pred = ridge.predict(X_test) mean_absolute_error(y_test, y_pred) 
mean_squared_error(y_test, y_pred) 
r2_score(y_test, y_pred) 
#regularization strength, often denoted as alpha
#L2 regularization penalty
#A larger alpha value results in stronger regularization, which tends to
#shrink the coefficients towards zero
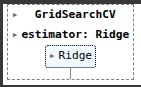
param_grid = { 'alpha' : [0.001, 0.01, 0.1, 1.0, 10.0, 100.0] } from sklearn.model_selection import GridSearchCV ridge_cv = GridSearchCV(ridge, param_grid, cv=3, n_jobs=-1) ridge_cv.fit(X_train, y_train) 
y_pred = ridge_cv.predict(X_test) mean_absolute_error(y_test, y_pred) 
mean_squared_error(y_test, y_pred) 
r2_score(y_test, y_pred) 
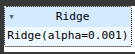
ridge_cv.best_estimator_ 
ridge3 = Ridge(alpha=0.001) ridge3.fit(X_train, y_train) 
ridge3.intercept_ 
ridge3.coef_ 
#if a coefficient was zero, then the lasso model would disregard it
