Poisson distribution in python
import numpy as np
from scipy.stats import poisson
import matplotlib.pyplot as plt
import seaborn as sns
Example 1 generate Poisson-Distributed Random Variables Numpy
lambda_value = 5 # mean number of occurrences (λ)
size = 10 # number of samples to generate
poisson_samples = np.random.poisson(lam=lambda_value, size=size)
print(poisson_samples)
Example 2 generate Poisson-Distributed Random Variables Scipy
poisson_samples_2 = poisson.rvs(mu=lambda_value, size=size, random_state=11)
print(poisson_samples_2)
poisson_samples_2.mean()
poisson_samples_2.std()
Example 3 Calculating Poisson Probability Mass Function (PMF) Part 1
# is a function that gives the probability that a discrete random variable is exactly
#equal to a particular value. In other words, the PMF describes the distribution of a
#discrete random variable by mapping each possible outcome to its corresponding probability
lambda_value = 5 # mean number of occurrences (λ)
k = 3 # number of events
# Calculate the probability of exactly k events given an average per year
probability = poisson.pmf(k, lambda_value)
print(probability)
#Example 4 Calculating Poisson Probability Mass Function (PMF) Part 2 #lam and mu are the same #array of values
probability2 = poisson.pmf(poisson_samples, mu=lambda_value)
print(probability2)
Example 5 Calculating Cumulative Distribution Function (CDF) - single point
lambda_value = 5 # mean number of occurrences (λ)
k = 3 # number of events
cumulative_probability = poisson.cdf(k, lambda_value)
print(cumulative_probability)
Example 6 Calculating Cumulative Distribution Function (CDF) - multiple
cumulative_probability2 = poisson.cdf(poisson_samples, lambda_value)
print(cumulative_probability2)
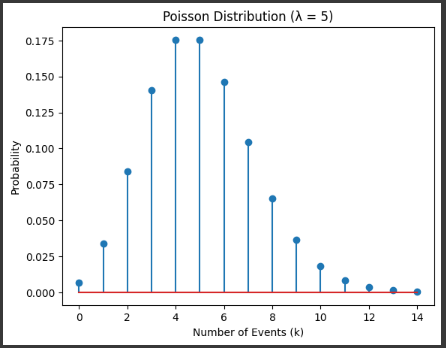
Example 7 Plotting a Poisson Distribution
lambda_value = 5 # mean number of occurrences (λ)
k_values = np.arange(0, 15) # range of k values
pmf_values = poisson.pmf(k_values, lambda_value)
plt.stem(k_values, pmf_values)
plt.title(f"Poisson Distribution (λ = {lambda_value})")
plt.xlabel('Number of Events (k)')
plt.ylabel('Probability')
plt.show()
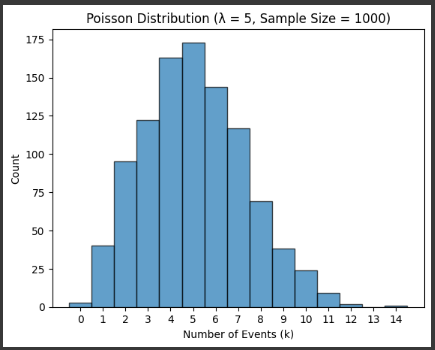
Example 8 Histogram
lambda_value = 5 # mean number of occurrences (λ)
sample_size = 1000 # number of samples to generate
data = np.random.poisson(lambda_value, sample_size)
# Create the histogram of counts
plt.hist(data, bins=np.arange(0, 16) – 0.5, edgecolor=’black’, alpha=0.7)
plt.title(f”Poisson Distribution (λ = {lambda_value}, Sample Size = {sample_size})”)
plt.xlabel(‘Number of Events (k)’)
plt.ylabel(‘Count’)
plt.xticks(np.arange(0, 15))
plt.show()
