Lasso Regression
#LASSO stands for Least Absolute Shrinkage and Selection Operator
#L1 regularization
#address overfitting – A model that is too complex may fit the training data very well
#but perform poorly on new, unseen data
#will get rid ofe useless features (make coefficients independent var next to 0)
#- automatic feature selection
# lead to a simpler model that is less prone to overfitting
https://www.youtube.com/watch?v=VqKq78PVO9g&ab_channel=codebasics 1:24
from sklearn.datasets import fetch_california_housing #https://inria.github.io/scikit-learn-mooc/python_scripts/datasets_california_housing.html
ca_housing = fetch_california_housing() X = ca_housing.data y = ca_housing.target ca_housing.feature_names 
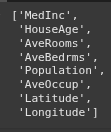
ca_housing.target_names 
from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=19) #Lasso regularization is sensitive to the scale of the features,
#so it’s a good practice to standardize the data to have zero mean and unit variance.
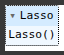
from sklearn.preprocessing import StandardScaler scaler = StandardScaler() X_train = scaler.fit_transform(X_train) X_test = scaler.transform(X_test) from sklearn.linear_model import Lasso lasso = Lasso() lasso.fit(X_train, y_train) 
from sklearn.metrics import mean_absolute_error, mean_squared_error, r2_score y_pred = lasso.predict(X_test) mean_absolute_error(y_test, y_pred) 
mean_squared_error(y_test, y_pred) 
r2_score(y_test, y_pred) 
#apply a param grid
#Alpha controls the strength of the regularization penalty
#You can fine-tune the alpha parameter to control the strength of the regularization penalty.
#Smaller values of alpha will result in less regularization,
#while larger values will increase the regularization effect and drive more coefficients to zero.
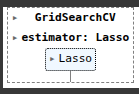
param_grid = { 'alpha' : [0.001, 0.01, 0.1, 1.0, 10.0, 100.0] } from sklearn.model_selection import GridSearchCV lasso_cv = GridSearchCV(lasso, param_grid, cv=3, n_jobs=-1) lasso_cv.fit(X_train, y_train) 
y_pred = lasso_cv.predict(X_test) mean_absolute_error(y_test, y_pred) 
mean_squared_error(y_test, y_pred) 
r2_score(y_test, y_pred) 
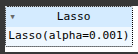
lasso_cv.best_estimator_ 
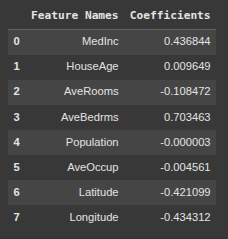
lasso3.intercept_ 
lasso3.coef_ 
#if a coefficient was zero, then the lasso model would disregard it
import pandas as pd feature_names = ['MedInc', 'HouseAge', 'AveRooms', 'AveBedrms', 'Population', 'AveOccup', 'Latitude', 'Longitude'] df = pd.DataFrame({'Feature Names': feature_names, 'Coefficients': lasso3.coef_}) df 
