Elastic Net Regressor
Elastic Net regression is a linear regression method that merges the strengths of both Lasso (L1) and Ridge (L2) regression techniques. It helps reduce overfitting and is especially effective when working with datasets that have many features, particularly when some of those features are highly correlated. The model’s regularization is controlled by two key hyperparameters: alpha (overall strength of regularization) and li_ratio (the balance between L1 and L2 penalties).
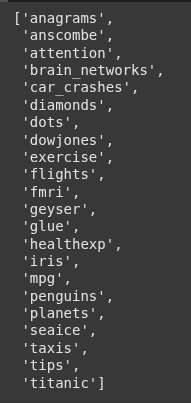
import seaborn as sns import pandas as pd sns.get_dataset_names() is a function from the Seaborn library that returns a list of dataset names available in Seaborn’s built-in dataset repository.
sns.get_dataset_names() 
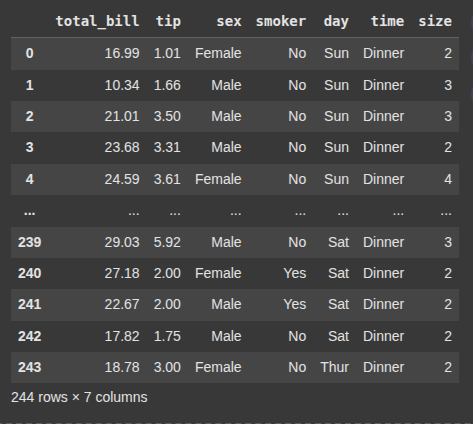
This loads the “tips” dataset from Seaborn’s built-in collection into a DataFrame called tips.
tips = sns.load_dataset("tips") tips 
This converts categorical columns in the tips DataFrame into one-hot encoded columns using pandas.
tips = pd.get_dummies(tips) This creates the feature matrix X by dropping the target variable (‘tip’) from the tips DataFrame
X = tips.drop('tip', axis=1) This extracts the target variable (tip) from the tips DataFrame and stores it in y.
y = tips['tip'] This imports the train_test_split function from scikit-learn, it is used to split your dataset into training and testing subsets.
from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=19) from sklearn.preprocessing import StandardScaler Here we import the StandardScaler class from scikit-learn, which is used to standardize features by removing the mean and scaling to unit variance.
scaler = StandardScaler() Here we fit the StandardScaler to the X_train data. i.e it calculates the mean and standard deviation for each feature.
X_train = scaler.fit_transform(X_train) After this we scale the test data, we should only transform it using the same scaler. we do not fit again, to prevent data leakage.
X_test = scaler.transform(X_test) Here we import the ElasticNet regression model from scikit-learn’s linear model module.
from sklearn.linear_model import ElasticNet elastic_net = ElasticNet() Here we fit the X_train, y_train to the ElaticNet() model.
After training we make predictions (i.e evaluate our models performance using .predict()).
elastic_net.fit(X_train, y_train) 
y_pred = elastic_net.predict(X_test) Next we import three key evluation metrics for regression models.
mean_absolute_error (MAE)
Measures the average of the absolute differences between predicted and actual values.
Lower is better.
Example: “On average, the model is off by X units.”
mean_squared_error (MSE)
Similar to MAE, but squares the errors—penalizes larger errors more.
Lower is better.
r2_score (R²)
Indicates how well the model explains the variability of the target.
Ranges from 0 to 1 (or can be negative if the model is worse than a horizontal line).
1.0 means perfect prediction.
from sklearn.metrics import mean_absolute_error, mean_squared_error, r2_score mean_absolute_error(y_test, y_pred) 
mean_squared_error(y_test, y_pred) 
r2_score(y_test, y_pred) 
li_ratio controls the balance between L1 (Lasso) and L2 (Ridge) regularization in Elastic Net. A value of 1 corresponds to pure Lasso, while 0 corresponds to pure Ridge.
To find the best model performance, it’s important to experiment with different values of alpha (regularization strength) alongside l1_ratio
param_grid = { "alpha": [0.1, 0.3, 0.5, 0.7, 0.9], 'l1_ratio': [0.1, 0.3, 0.5, 0.7, 0.9],} we import the GridSearchCV, which is used to tune hyperparameters of a model by performing cross-validated grid-search.
from sklearn.model_selection import GridSearchCV elastic_cv = GridSearchCV(estimator=elastic_net, param_grid=param_grid, cv=3, scoring='neg_mean_squared_error', n_jobs=-1) Next, we fit the model using the best hyperparameters from GridSearchCV, make predictions, and evaluate its performance using our evaluation metrics. This helps us determine whether the tuned model performs better than the default one (i.e., without hyperparameter tuning).
elastic_cv.fit(X_train, y_train) 
y_pred = elastic_cv.predict(X_test) mean_absolute_error(y_test, y_pred) 
mean_squared_error(y_test, y_pred) 
r2_score(y_test, y_pred) 
