Python probability mass function
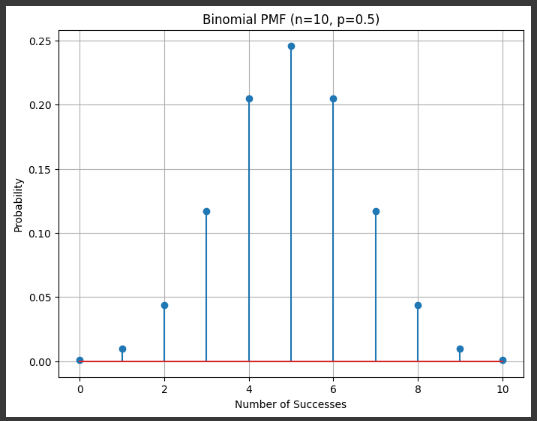
import numpy as np import matplotlib.pyplot as plt from scipy.stats import binom, poisson, geom, randint Example 1 Binom
success or failure, multiple trials each time
n = 10 # number of trials p = 0.5 # probability of success k = np.arange(0, n+1) pmf = binom.pmf(k, n, p) plt.figure(figsize=(8, 6)) plt.stem(k, pmf) plt.title(f'Binomial PMF (n={n}, p={p})') plt.xlabel('Number of Successes') plt.ylabel('Probability') plt.grid(True) plt.show() 
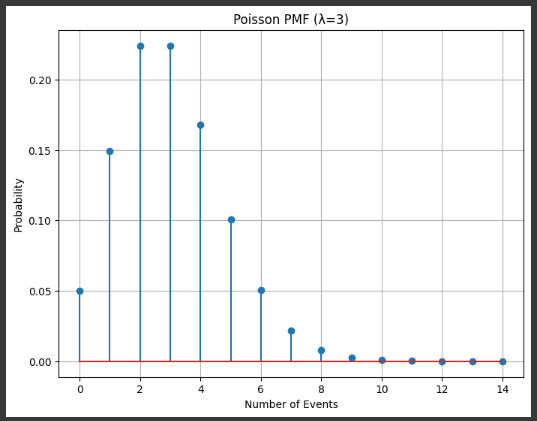
Example 2 Poisson
number of events happening in a fixed interval of time
lambda_poisson = 3 # average rate k = np.arange(0, 15) pmf = poisson.pmf(k, lambda_poisson) plt.figure(figsize=(8, 6)) plt.stem(k, pmf) plt.title(f'Poisson PMF (λ={lambda_poisson})') plt.xlabel('Number of Events') plt.ylabel('Probability') plt.grid(True) plt.show() 
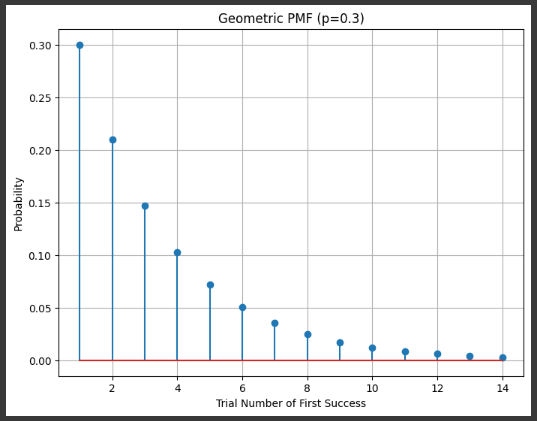
Example 3 Geometric
trials till first success
p_geom = 0.3 # probability of success k = np.arange(1, 15) pmf = geom.pmf(k, p_geom) plt.figure(figsize=(8, 6)) plt.stem(k, pmf) plt.title(f'Geometric PMF (p={p_geom})') plt.xlabel('Trial Number of First Success') plt.ylabel('Probability') plt.grid(True) plt.show() 
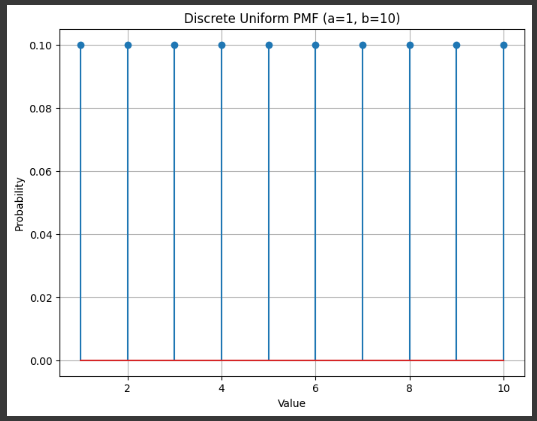
Example 4 Uniform
equal likelyhood of result
# Parameters a_uniform = 1 # lower bound b_uniform = 10 # upper bound # Range of possible values k = np.arange(a_uniform, b_uniform + 1) # PMF values pmf = randint.pmf(k, a_uniform, b_uniform + 1) # Plotting plt.figure(figsize=(8, 6)) plt.stem(k, pmf) plt.title(f'Discrete Uniform PMF (a={a_uniform}, b={b_uniform})') plt.xlabel('Value') plt.ylabel('Probability') plt.grid(True) plt.show() 
