uniform distribution python
import numpy as np import matplotlib.pyplot as plt from scipy.stats import randint np.random.seed(11) Example 1 Random Numbers 0 to 1
data = np.random.uniform(size=250) print(data) 
Example 2 Generate Dice Rolls
n_rolls = 1000 rolls = np.random.randint(1, 7, size=n_rolls) print(rolls) 
Example 3 Data Points
# Calculate the mean, variance, and standard deviation mean_rolls = np.mean(rolls) print(mean_rolls) 
var_rolls = np.var(rolls) print(var_rolls) 
std_rolls = np.std(rolls) print(std_rolls) 
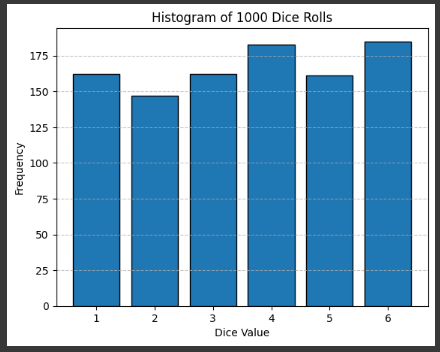
Example 4 Histogram Plot
# Plot the histogram plt.hist(rolls, bins=np.arange(1, 8) - 0.5, edgecolor='black', rwidth=0.8) plt.xlabel('Dice Value') plt.ylabel('Frequency') plt.title(f'Histogram of {n_rolls} Dice Rolls') plt.xticks(np.arange(1, 7)) plt.grid(axis='y', linestyle='--', alpha=0.7) # Show the plot plt.show() 
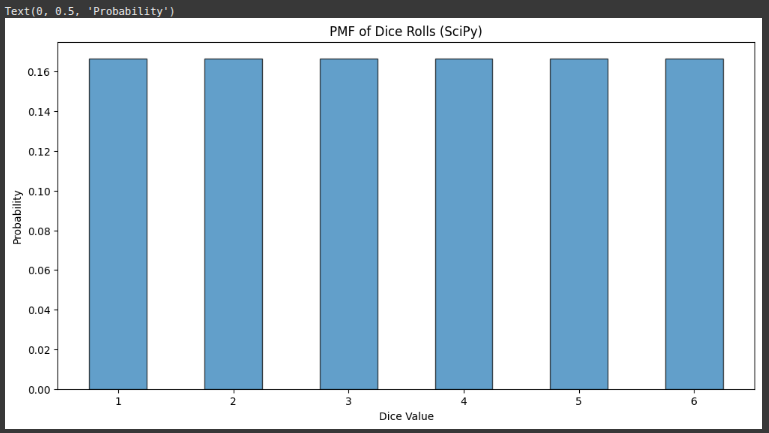
Example 5 Calculate PMF
dice_distribution = randint(1, 7) values = np.arange(1, 7) # Calculate the PDF using SciPy (for a discrete uniform distribution) pmf_scipy = dice_distribution.pmf(values) # Plot the PMF using SciPy plt.figure(figsize=(12, 6)) plt.bar(values, pmf_scipy, width=0.5, edgecolor='black', alpha=0.7) plt.title('PMF of Dice Rolls (SciPy)') plt.xlabel('Dice Value') plt.ylabel('Probability') 
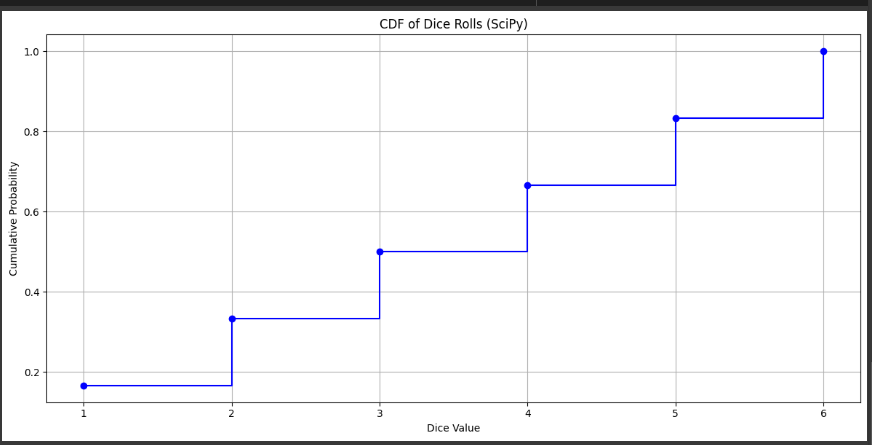
Example 6 Calculate CDF
# Calculate the CDF using SciPy cdf_scipy = dice_distribution.cdf(values) # Plot the CDF using SciPy plt.figure(figsize=(12, 6)) plt.step(values, cdf_scipy, where='post', label='CDF', color='b', marker='o') plt.title('CDF of Dice Rolls (SciPy)') plt.xlabel('Dice Value') plt.ylabel('Cumulative Probability') plt.grid(True) plt.tight_layout() plt.show() 
